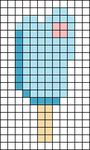
Dimensions
33x50
Strings
34
Colors
5
Rate Pattern
11 Similar patterns
1 Photo

#81959
by 5927001538
11 Comments
| You have to be Logged in to post a comment. |
| danielle_3 |
3 years, 9 months ago by danielle_3
@hellooooo haha their song is always in my head
|
| hellooooo |
3 years, 10 months ago by hellooooo
You can relaxColleen on Erik have a podcast The world is scary and we’re looked in our home And now we have big microphones You can relax that’s the name of our podcast |
| audreyb37 |
4 years, 1 month ago by audreyb37
LOL This is my fave podcast 😂
|
| danielle_3 |
4 years, 3 months ago by danielle_3
@5927001538 thanks for making the pattern it looks so good! 🤩
|
| 5927001538 |
4 years, 3 months ago by 5927001538
@danielle_3 thanks 😊
|
| danielle_3 |
4 years, 3 months ago by danielle_3
@ChaosZone yes the podcast is amazing!
|
| ChaosZone |
4 years, 3 months ago by ChaosZone
LOVE the podcast! So awesome 😍
|
| teponaztli |
4 years, 3 months ago by teponaztli
❤️
|
| danielle_3 |
4 years, 3 months ago by danielle_3
@PastelPony lol thank you!
|
| PastelPony |
4 years, 3 months ago by PastelPony
Literally, I tend to over stress a lot of things so it tell this to myself every day 😜 oh and really colorful and unique pattern!!
|